旋压钛材的变形原理

1 剪切旋压
A 正弦规律
异形件变薄旋压为剪切旋压变形，工件形状包括锥形件、曲母线形工件以及椭球体封头等。当芯模半锥角为α,旋压件壁厚为δ1时，旋压前后壁厚关系满足正弦规律公式6-2.
正弦规律公式是制定工艺参数和控制剪切变形的依据。锥形件剪切旋压是复杂的金属变形过程，可简化变形过程为理想变形状态，将坯料视为若干同心单元环组成。剪切旋压后，同心单元环产生轴向滑动，形成锥体同心环，即纯剪切变形状态。按照纯剪切变形原理，由板坯旋压锥形件时，其壁厚减薄率，与旋压件锥角之间存在下列关系：
Ψt=(δ0-δ1)/δ0=1-sinα         （6-4)
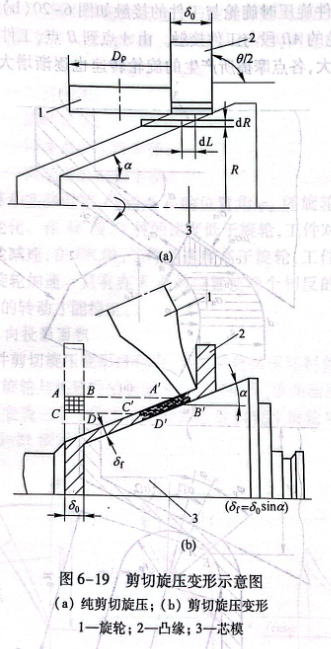
纯剪切应变等于单元体轴向滑动的距离除以单元体的厚度，即：y=dl/dR=cotα.凸缘垂直轴线时，即α=Θ/2=90°。如坯料为预成形件，预成形锥角Θ/2处于90°~0°之间，则剪切应变为y=cota-cot(0/2)。即在芯模锥角相同时，预成形锥角越小，则剪切应变越小。剪切旋压变形理想模型如图6-19(a)所示。纯剪切旋压时坯料没有周向收缩，只产生轴向的塑性流动，坯料变形前后任何点的半径距离均相等。
锥形件剪切旋压旋轮与坯料接触实际变形如图6-19(a）所示。坯料相邻线段AB、CD,即AB=CD=δ.变形后A'B'=C'D'=δ..变形表现为由ABCD矩形变成A'B'C'D'平行四边形，即AB相对CD平行错动，只有角度变化。
锥体在旋轮作用下除剪切变形外，还有沿周向的塑性流动，因坯料与芯模的摩擦作用，导致工件外表面应变硬化强于内表面。
锥形件由多道次剪切旋压成形时，半锥角αn半成品的壁厚δn、板坯壁厚δ0的正弦关系为sinαn=δn/δ0.

B 变形与摩擦
锥形剪切旋压件纵剖面如图6-20(a)所示，acde为剪切变形区。材料从de线开始变形，到ac线时结束，构成拉弯区域。拉弯区域由旋轮圆角半径对坯料施力p形成，并产生径向正应力σn和轴向剪应力To. abc三角区为主变形区域，主变形区域含拉应力σc..芯模对工件的正压力σm及摩擦力μσm.

锥形件旋压时旋轮与工件的接触如图6-20(b)所示。由图可知，旋轮的AB段与工件接触。由A点到B点，工件与旋轮半径比逐渐增大，各点摩擦所产生的旋轮转速也逐渐增大。在AB段

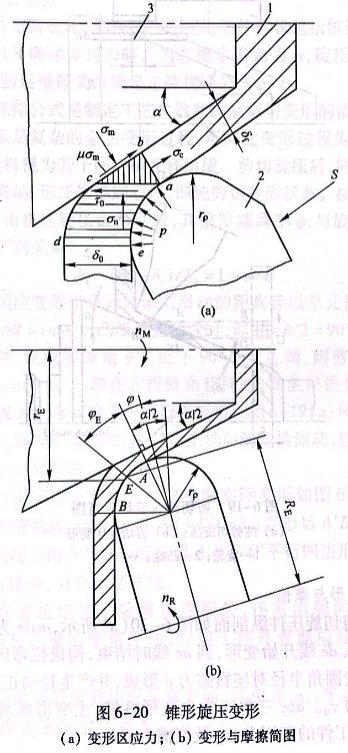
只有一个同速点，即工件的圆周速度与旋轮的圆周速度相等，此点为滚动摩擦，其余点为滑动摩擦。AB段中E点为同速点，即：nMrE=nRRE    （6-5)
式中
nM一工件转速；
nR-旋轮转速；
rE-同速点处工件半径；
RE一同速点处旋轮半径。
据计算和实测可知，同速点E的位置角随旋轮所处位置的不同而变化。在AE段，工件的速度低于旋轮，工件对旋轮的摩擦力使旋轮减速；在EB段，工件的速度高于旋轮，工件对旋轮的摩擦力使旋轮加速。只有在E点的位置使两个相反的摩擦力矩平衡，旋轮的转动才能稳定。
C 三向投影面积
锥形件剪切旋压变形过程中，旋轮圆角挤压坯料使其产生塑性变形时，旋轮与坯料的接触面为一空间曲面，该曲面沿三个方向分别投影，变为三个平面图形。锥形件剪切旋压旋轮与工件三面投影如图6-21所示。

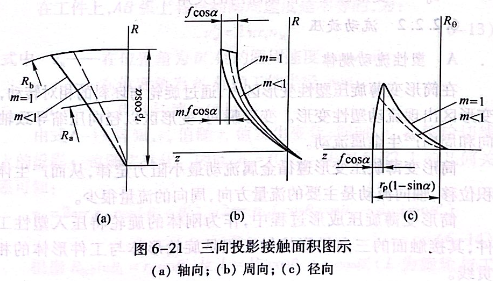
锥形件旋压时，旋轮与工件接触面简化后的投影分别为abc、a'b'c'和a"b"c"。径向H、轴向L、周向B三个边长计算公式分别为：
H=fcosa                         （9-9)
L=rp(1-sina)                      （6-7)
B=rpcosα                        （6-8)
式中
f-旋轮进给比，mm/r;
rp-旋轮圆角半径，mm.
由作图法可导出三个投影图形的轮廓数值，根据解析法近似计算，可求出三向投影接触面积。三向投影面积简化计算公式分别为：
AΘ=1/2fr,cos2α                       （6-9)
AR=1/2rp(1-sina)roθ0                   （6-10)
AL=1/2rpcosar0θ0                      （6-11)
式中
Aθ-周向接触面积；
AR-径向接触面积；
AL-轴向接触面积；
r0-变形区的工件半径；
θ0-变形区在工件截面内的夹角。
2 流动旋压
A塑性流动规律
在筒形变薄旋压塑性变形区内，通过旋轮与坯料的相对转动，变形区出现流动塑性变形。变形瞬间，变形区以径向压缩导致轴向和周向产生金属流动。
筒形变薄旋压变形遵循金属流动最小阻力定律，从而产生体积位移，轴向流动是主要的流量方向，周向的流量很少。
筒形变薄旋压成形过程中，作为刚体的旋轮将压入塑性工件，其接触面的三向投影接触面积是旋轮形体与工件形体的相贯线。
旋轮与工件的接触区如图6-22所示，可对旋轮与工件接触区的任一横断面N-N上的摩擦力进行分析。

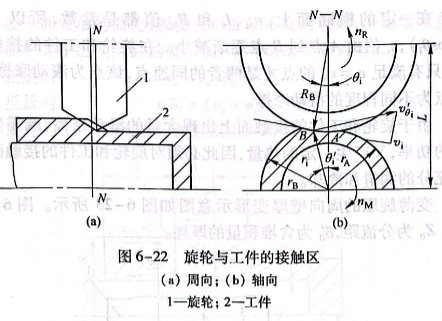
由图6-22可以看出，横断面的旋轮与工件接触于AB弧。在AB弧上，旋轮上每一点的圆周速度是相等的，即：
VN=2πRNnR                    （6-12)
式中
VN-N-N截面上旋轮的圆周速度，mm/min;
RN-N-N截面上旋轮的半径，mm.
在工件上，AB弧上各点的圆周速度是不等的，为：
vΘ’=2πrinM                   （6-13)
式中
vΘ’一在位置角为Θi’处的圆周速度，mm/min;
ri-在位置角为Θi’;处的工件半径，mm;
nM-工件的转速，r/min.
由式6-13可知，vΘ’值随r;值发生变化；同时，在旋轮切线上的投影v;也随之变化。因此，vi=f(ri)。由图6-22上的几何关系可知：
vi=2πrinmcos(θi+θi’) =2πrinм(cosθicosθi’ - sinθisin0i’)           (6-14)
根据RNsinθi =risinθi’及L = RNcosθi +ricosθi’ (L为旋轮与工件的中心距），式6-14可简化为：
vi=2πnM(Lcosθi-RN)                  （6-15)

在一定的横断面上，nM、L和RN值都是常数，所以v;=f(cosθ;),vi值由A点到B点逐渐减小。在旋轮和工件的接触面上，只有满足vi=VN的点才是两者的同速点，该点为滚动摩擦，其余点为不同程度的滑动摩擦。
由于旋轮和工件的接触面上出现大量的滑动摩擦，既需要较大的功率，又产生一定的热量，因此必须对旋轮和工件的接触面进行充分的润滑和冷却。
变薄旋压的周向壁厚变形示意图如图6-23所示。图6-23中，Z0为分流距，δ0’为含堆积量的厚坯。

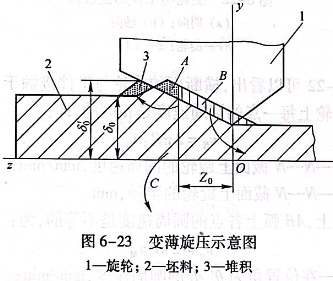
从图6-23剖面分流图可以看出，在工件被旋轮碾压一圈的体积中，以距y轴为Z.的分流线为界，面积B的金属向后流向旋压件的壁部，面积A的金属向前流动形成隆起与堆积。箭头C表示有少量金属沿周向流动。金属隆起与堆积导致8.增至86,增大变形量与变形力。当隆起量不变时，旋压变形基本稳定。
B 变形与摩擦
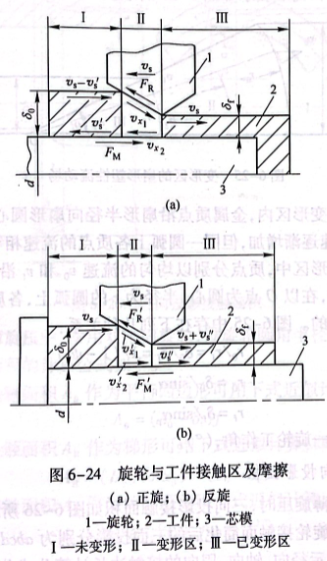
在筒形件变薄旋压塑性变形过程中，无论正旋与反旋，旋轮与工件的接触面存在着强烈的滑动摩擦。变形区由已变形区向未变形区推进，稳定流动时，单位时间流入变形区的金属量等于流出变形区的金属量。

经平面变形的简化，根据变形面积不变的假设，未变形区参与变形面积等于已变形区的变形面积，可得出下列关系式：

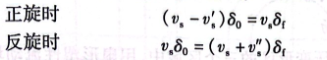
旋轮与工件接触区及摩擦如图6-24所示。

在变形区，金属正旋与反旋塑性流动的摩擦阻力分别为FR与，就旋轮而言，均向着床头方向。就芯模而言，金属塑性流动的摩擦阻力FM与F'M在正旋与反旋不同过程中方向相反。变薄旋压时，材料综合了压缩、拉伸和剪切的复合变形。受变形量和摩擦阻力的影响，金属畸变程度靠近旋轮处变形量较大，靠近芯模处变形量较小。
C 塑性流动场
在筒形变薄旋压变形区的三个区域中，用扇形塑性流动场对材料的流动和变形表示如图6-25所示。

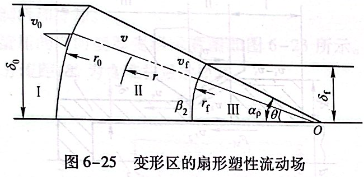
在扇形变形区内，金属质点沿扇形半径向扇形圆心0点方向流动，其流速逐渐增加，但同一圆弧上各质点的流速相等。在未成形区和已成形区中，质点分别以均匀的流速和沿轴向流动。
在变形区中，在以0点为圆心，半径为r的圆弧上，各质点的流动速度是相等的。图6-25中存在下列几种关系：
ro/rf=δ0/δ1=1/(1-Ψt)
ro=δ0/sinap
rf=δf/sinap
式中
αp一旋轮工作角，（°).
D 三向投影面积
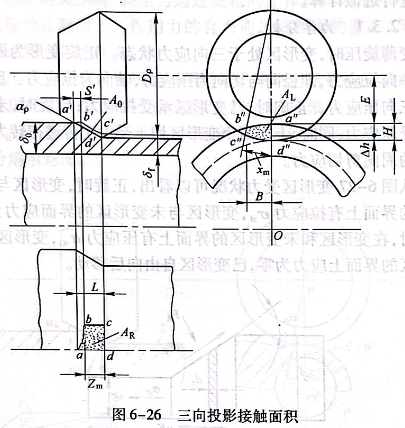
筒形变薄旋压时，三向投影接触面积如图6-26所示。
工件与旋轮接触面简化后的三面投影分别为abcd、a'b'c'd'和＂b"c"d"。图示径向、轴向、周向的接触边长计算公式分别为：
H=δ0-δf                                （6-16)
L=(δ0-δf)cotp                           （6-17)
B=[(Dp-f'tanαp)f’tanαp]1/2              （6-18)
式中
Dp-旋轮直径，mm.

在变薄旋压中，常用双锥面旋轮，设旋轮圆角半径rp≈0，三向投影接触面积的计算公式如下。
周向接触面积AΘ作为平行四边形可用下式近似计算，即：
AΘ=(δ0-δf)f                          （6-19)
径向接触面积AR作为梯形可用下式近似计算，即：
AR=(Dpfcotαp)1/2(δ0-δf)             （6-20)
轴向接触面积AL作为长方形可用下式近似计算，即：
AL=(δ0-δf)(D.ftana)1/2               （6-21)

本公司主要产品：钛棒、钛管、钛板、钛阳极、钛箔钛带、钛法兰、钛丝、钛靶材、钛设备、钛饼钛环、钛标准件、钛加工件